Die Griechische Bildhauer versuchten bewusst, das Verhältnis des Goldenen Schnitts mehrfach in die Abmessungen zum Beispiel dieser Statue einzuarbeiten um die Dynamik der menschlicher Körperhaltung zu zeigen.
http://www.khg.bamberg.de/Der Mensch ist mehr als die Summe seiner Teiler, sein Körperbau ist das Ebenbild der Verhältnissen des goldenen Schnittes und seiner Bewegungen entstehen als die Ebenbilder des Weges der dynamischen goldenen Spiralen. Der Mensch mit seinem Körper und seiner Seele, mit seinen Emotionen, seinen Gedanken, seinen Empfindungen und seinen Bewegungen ist von Anfang der Evolution mit dem Gesetz und den Verhältnissen des goldenen Schnittes verknüpft. Aus diesem Harmonie Gesetz, der in sich alle vier Dimensionen menschlichen Daseins vebiergt, entstehet auch die menschliche Gesundheit.
In der Kinesitherapie ist die Herstellung der Geometrie des Körpers die Vorausstzung für die Schmerzbekämpfung des Bewegungssystems. Ich suchte die Wege wie ich dem Patient die Wahrnehmung seiner Körper- Bewegunsgeometrie bei brinngen könnte um ihm in die vierte Dimension seines Daseins einführen zu können. Ich schrieb meinen Buch "Die Kreativitäten der alltägliche Bewegung" und arbeitete an meiner Methode "Manu propria Kinestherapie". Die Dynamik der goldene Spirale zeigte mir den Weg in meine vierte Dimension und ich versuchte durch die 4- D Eigenmobilisation meine eigene Körper- Bewegunsgeometrie wahrzunehmen.
http://die.tore.der-zeit.blogspot.com/Was ist die Geometrie?
Einerseits versteht man unter "Geometrie" die zwei- und dreidimensionale euklidische Elementargeometrie, die auch im Schulunterricht gelehrt wird und die sich mit Punkten, Geraden, Ebenen, Abständen, Winkeln etc. beschäftigt, sowie diejenigen Begriffsbildungen und Methoden, die im Zuge einer systematischen und mathematischen Behandlung dieses Themas entwickelt wurden.
Andererseits umfasst der Begriff „Geometrie" eine Reihe von grossen Teilgebieten der Mathematik, deren Bezug zur Elementargeometrie für Laien nur mehr schwer erkennbar ist.
Obwohl allgemein angenommen wird, dass die Schulung des räumlichen Denkvermögens für die Entwicklung der menschlichen Intelligenz von grosser Bedeutung ist, führt die Raumgeometrie im Schulunterricht ein Schattendasein. In der Oberstufe wird zwar analytische Geometrie unterrichtet, dies geschieht aber oft auf einem sehr abstrakten Niveau. Die Raum und Bewegungsgeometrie unseres Körpers müssen wir Denkenlernen. Die Ideokinese, ist eine Methode die bildhafte Vorstellungen verwendet, um uns das räumlichen und beweglichen Denkvermögen zu erleichtern.
http://ideokinese.blogspot.com/Heute ist dynamische geometrie auf dem Computer ein wichtige teil der Geometrie geworden, weil die uns ermöglicht die Bewegungen im Raum bewusst wahr zu nehmen.
Die Kinematik (gr.: kinema, Bewegung) ist die Lehre von der Bewegung von Punkten und Körpern im Raum.
Biokinematik ist ein Begriff aus der Kinesiologie oder deutsch Bewegungslehre und Bewegungswissenschaft, der in der Biologie, Sportwissenschaft und Sportmedizi, die Anwendung findet. Dabei wird die Lehre von den bewegten Körpern aus der Mechanik auf lebende Objekte angewandt. Die Biokinematik ist Teil einer wissenschaftlich orientierten Bewegungsanalyse und untersucht Änderungen des Bewegungzustandes. Sie beschreibt die räumliche und zeitliche Charakteristik der Bewegung, ohne die Masse der sich bewegenden Körper und die auf sie einwirkenden Kräfte zu berücksichtigen. Messgrössen der Biokinematik sind Ort, Weg, Zeit, Geschwindigkeit und Beschleunigung.
Die Quadratur des Kreises
In der Antike beschäftigten sich zahlreiche Mathematiker mit der Frage, wie und ob mit Hilfe einer geometrischen Konstruktion, welche ausschliesslich Lineal und Zirkel verwendet, ein Quadrat in einen flächengleichen Kreis (und umgekehrt) verwandelt werden kann.
Die berühmte Zeichnung
"Proportionsstudie nach Vitruv" von Leonardo da Vinci (1452-1519) enthält ein erst jetzt entdecktes mathematisches Geheimnis.
Wie der Münsteraner Mathematiker Klaus Schröer und der Kunsthistoriker Dr. Klaus Irle nachweisen, ist in dem Kunstwerk ein Lösungsvorschlag für das im 15. Jahrhundert berühmteste mathematische Problem, die so genannte Quadratur des Kreises, chiffriert. Diese Aufgabe verlangt, nur mit einem Zirkel und einem masslosen Lineal ein flächengleiches Paar Kreis und Quadrat zu konstruieren.
"Ich qudriere den Kreis"
Leonardo da Vinci hat sich Zeit seines Lebens mit keiner anderen mathematischen Aufgabe so intensiv beschäftigt wie mit dieser.
"Ferner ist natürlicherweise der Mittelpunkt des Körpers der Nabel. Liegt nämlich ein Mensch mit gespreizten Armen und Beinen auf dem Rücken, und setzt man die Zirkelspitze an der Stelle des Nabels ein und schlägt einen Kreis, dann werden von dem Kreis die Fingerspitzen beider Hände und die Zehenspitzen berührt. Ebenso, wie sich am Körper ein Kreis ergibt, wird sich auch die Figur eines Quadrats an ihm finden. Wenn man nämlich von den Fusssohlen bis zum Scheitel Mass nimmt und wendet dieses Mass auf die ausgestreckten Hände an, so wird sich die gleiche Breite und Höhe ergeben, wie bei Flächen, die nach dem Winkelmass quadratisch angelegt sind.“ Vitruvius
Mit seiner Federzeichnung illustriert Leonardo da Vinci also, allerdings nicht als Erster, die These des Vitruvius, der aufrecht stehende Mensch füge sich sowohl in die geometrische Form des Quadrates wie des Kreises ein.
Wie auf der Zeichnung ersichtlich, setzt der Künstler für den "homo ad circulum" den Zirkel tatsächlich exakt im Nabel an. Beim „homo ad quadratum“ ist dagegen der Schritt der exakte Mittelpunkt des Quadrates.
Das Idealbild der menschlichen Schönheit ist daher kein absolutes, sondern besteht aus der Beziehung einzelner Teile zueinander, wie es auch der goldene Schnitt fordert.
Die einzige zu dieser Zeichnung erschienene und nach einem Leonardozitat benannte Werkmonografie „Ich aber quadriere den Kreis ...“ kam 1998 zu dem ungewöhnlichen Schluss, dass die Doppelfigur in Kreis und Quadrat einen Lösungsvorschlag Leonardos zur in endlich vielen Konstruktionsschritten unmöglichen
Quadratur des Kreises darstellt (letzteres wurde auf der Basis der
Galoistheorie von
Ferdinand von Lindemann 1882 zweifelsfrei bewiesen).
Die moderne Mathematik hat nachwiesen dass diese Aufgabe theoretisch unlösbar ist.
Der Satz des Pythagoras
Den Ägyptern und Babyloniern war schon vor mehr als 4000 Jahren bekannt, dass ein Dreieck mit den Seitenverhältnissen von 3 : 4 : 5 rechtwinklig ist. Sie wandten dies an, indem sie eine Schnur in zwölf gleiche Stücke unterteilten und die Schnur dann so zu einem Dreieck auslegten, dass eine Seite aus drei Stücken, eine zweite aus vier, und die dritte Seite aus fünf Stücken gebildet wurde. So konnten sie mit kleinem Aufwand einen rechten Winkel konstruieren.
Etwa 500 Jahre vor Christus lebte in Griechenland ein Gelehrter namens Pythagoras. Er kannte besonderen Dreiecke, die rechtwinklig sind, wenn ihre Seitenzahlen in einem speziellen Verhältis zueinander stehen. Er erforschte sie systematisch und fand heraus, dass die Summe der Quadrate der beiden kürzeren Seiten das Quadrat der längeren Seite ergibt. Es gelang ihm auch zu beweisen, dass dies nicht nur für spezielle rechtwinklige Dreiecke gilt, sondern allgemeingültig ist. Heute schreiben wir das so: a2 + b2= c2.
Der Goldene Schnitt
a verhält sich zu b wie a+b zu a
Man muss kein Mathematiker sein, kein Baumeister, kein Architekt oder Künstler, um der Faszination der "göttlichen Teilung", wie das Mass auch genannt wird, zu erliegen. Dabei ist der Goldene Schnitt zuächst mal nichts anderes als ein Zahlenverhältnis, ausgedrückt in der irrationalem Zahl Phi.
Die Geschichte des Goldenen Schnitts.
Von einigen Historikern wird angenommen, dass die Pythagoreer, Anhänger der Schule des Pythagoras, im 5. Jahrhundert v. Chr. als erste mit Hilfe des Goldenen Schnittes inkommensurable Strecken entdeckten. Diese Strecken sind die geometrischen Äquivalente der irrationalen Zahlen. Die Pythagoreer haben schon damals festgestellt dass die Natur keine gerade Linien und keine Ruhe kennt.
Seit der Antike waren Künstler, Philosophen und Mathematiker von der Schönheit, Genauigkeit und Gültigkeit des Goldenen Schnittes fasziniert.
Dabei hatte der Schnitt in der antiken Welt noch keinen Namen. Er war einfach da und man konnte ihm überall in der Natur beobachten und wahrnehmen. Erst später wurde er dann mit "proportio habens medium et duo extrema", was heisst so viel wie: "Teilung im äusseren und mittleren Verhältnis", beschrieben.
Wegen des ästhetischen Eindrucks auf den Betrachter wird er in der Architektur und der Kunst seit der Renaissance auch
harmonische Teilung genannt.
In der Nachfolge Pythagoras' (ca. 575- ca. 500 v. Ch.) interpretierten die Pythagoreer Zahlen als "Quelle ethischer und ontologischer Erkenntnis." Doch meinten sie immer natürliche Zahlen (arithmoi). In der "wohl geordneten pythagoreischen Zahlenwelt gibt es für irrationale Zahlen und Verhältnisse keinen Ort." Deshalb passte das Massverhältnis des Goldenen Schnitts nicht so richtig in ihr "Weltbild", denn es lässt sich nicht mit ganzen Zahlen darstellen, und sie gaben ihm die Name Phi.
Hippasos, der Sohn des Pythagoras, erforschte als einer der ersten den Zusamenhang des goldenes Schnittes mit dem Fünfeck. 
Die Pytagoreer massen dem Fünfeck, auch Fünfalfa genannt, die geheimnisvolle Kräfte und Eigenschaften zu. So wurde das Pentagramm Symbol der Gesundheit.
Für die Konstruktion verwendete man damals den sog. Goldenen Zirkel, ein mechanisches Instrument, mit dem man den Goldenen Schnitt bestimmen und überprüfen kann.
Der Goldene Schnitt ist ein Grössenverhältnis in der Geometrie, das zahlreichen Entwicklungsformen in der Natur zugrunde liegt, von der Spirale der Nautilusmuschel bis zu den Blütenblättern der Sonnenblume, taucht es in vielen Dingen auf, die wir als schön empfinden.
Von den alten Griechen entdeckt und durch den griechischen Buchstaben PHI dargestellt, repräsentiert der Goldene Schnitt die irrationale Zahl 1.618. In Kunst und Architektur gilt dieses Verhältnis als eine gewissermassen optimale Proportion, die auf unsere ästhetische Rezeption wirkt.
Der Goldene Schnitt ist Kennzeichen des stendigen Wachstum in der Natur und dessen, was uns als Harmonie und Schönheit erscheint. Die Natur entwickelt sich der Gesetz des goldenen Schnitts folgend.
Seine Anwendung geht zurück auf die alten Ägypter und Griechen, die es im Bau von Tempeln und Pyramiden einsetzten. Künstler und Architekten verwendeten dieses Verhältnis zu allen Zeiten bei Aufbau und Zusammensetzung ihrer Gebäude, Gemälde um ihren Werken ein Gefühl der natürlichen Ästhetik, Ordnung und Schönheit zu vermitteln.
Fibronacci- Zahlen
Ihren Ursprung hat diese Zahlenfolge in einem eher trivialen Problem, einer von vielen Rechenaufgaben, die Fibonacci in seinem Liber abaci behandelt: der sogenannten Kaninchenaufgabe. Bei Fibonacci selber ist allerdings die erste 1 der Folge nicht berücksichtigt.
"Wieviele Kaninchenpaare entstehen im Verlauf eines Jahres aus einem Paar? Ein Mann hielt ein Paar Kaninchen an einem Ort, der ringsum von einer Mauer umgeben war, um herauszufinden, wieviele Paare daraus in einem Jahr entstünden. Dabei ist es ihre Natur, jeden Monat ein neues Paar auf die Welt zu bringen, und sie gebären erstmals im zweiten Monat nach ihrer Geburt. Weil das obengenannte Paar schon im ersten Monat gebiert, kannst du es verdoppeln, so dass nach einem Monat zwei Paare da sind. Von diesen gebiert eines, d.h. das erste, im zweiten Monat wieder; und so gibt es im zweiten Monat 3 Paare. Von denen werden in einem Monat 2 wieder trächtig, so dass im dritten Monat zwei Kaninchenpaare geboren werden; und so sind es dann in diesem Monat 5 Paare. Von denen werden im selben Monat 3 trächtig, so dass es im vierten Monat 8 Paare sind. Von diesen gebären 5 Paare wieder 5 Paare; wenn man diese zu den 8 Paaren addiert, ergeben sich im fünften Monat 13 Paare. "
In der Reihe der Fibonacci-Zahlen lässt sich auch der Goldene Schnitt aufspüren. Die Rede ist von der auf einen berühmten Mathematiker des 13. Jahrhunderts zurückgehenden unendlichen Zahlenreihe 1, 1, 2, 3, 5, 8, 13, 21, 34.............
Teilt man die jeweils aufeinander folgenden Fibonacci-Zahlen, erhält man eine Folge von Brüchen:
1/1, 1/2, 2/3, 3/5, 5/8, 8/13, 13/21... Diese Folge nähert sich, je höher Nenner und Zähler der Brüche werden, immer weiter der Zahl Φ Phi 1,6 des Goldenen Schnitts an.
Unabhängig von Fibonacci beschäftigte sich auch der deutsche Astronom und Mathematiker Johannes Kepler (1571-1630) mit der Zahlenfolge 1, 2, 3, 5, 8, 13, 21 ..., wenn auch in einem ganz anderen Kontext.
In seinem Werk über die Weltharmonik, Harmonices Mundi (1619), kommt Kepler im Zusammenhang mit der Sphärenmusik und den Verhältnissen von Tonintervallen auf den Goldenen Schnitt, die "proportio divina", zu sprechen. Er findet darin die "schöne Idee einer Fortzeugung".
Wenn man den grösseren Teil einer nach dem Goldenen Schnitt geteilten Strecke zum Ganzen hinzuaddiere, so stehe die Summe zu dieser Strecke wiederum im Verhältnis des Goldenen Schnitts. Dieses Verhältnis könne zwar nicht in rationalen Zahlen ausgedrückt werden, doch gebe es eine Zahlenfolge, die sich kontinuierlich dem wahren Wert annähere. Dann führt Kepler die ersten Zahlen der Fibonacci-Folge auf (1, 2, 3, 5, 8, 13, 21 ...) und erläutert die Gesetzmässigkeit der Bildung ihrer Glieder als Summe der zwei vorhergehenden Zahlen, die sich bis ins Unendliche fortsetzen lasse. Er beobachtet ferner, dass sich das Quadrat einer Zahl dieser Folge jeweils um 1 vom Produkt der beiden benachbarten Zahlen unterscheidet, wobei die Differenz abwechselnd positiv oder negativ ist.
Damit formuliert Kepler ebenfalls die Approximation, des Goldenen Schnitts durch die Verhältnisse aufeinanderfolgender Fibonacci-Zahlen.
Manifestationen der Fibonacci-Reihe finden wir beispielsweise in den Spiralen von Schnecken, Muscheln, in der Anordnung der Kerne in Sonnenblumen oder bei Tannenzapfen und auch in den kleinsten teilchen unseres Gehirns in den Mikrotubuli seiner Neuronen.
Namhafte theoretische Physiker Roger Penrose wagte sich in seinem Buch "Schatten des Geistes" gar an eine These über die Entstehung des Bewusstseins: Dieses basiere auf Quantenphänomenen in den Mikrotubuli der Nervenzellen. Penrose interessiert sich für die fundamentalen Prozesse in unserem Kopf, für den Punkt, an dem Geist auf Materie trifft. Und dazu hat er einige Ideen, die er in diversen Bücher darlegt. Schatten des Geistes ist eines davon und ich erinnere mich nur noch an den hübschen Gedanken, dass Mikrotubuli nach Fibonacci-Zahlen aufgebaut sind. Unser Bewusstsein in seinem Werdegang befolgt auch das Gesetz des goldenen Schnittes.
Der goldene Schnitt zeigt die stetige Teilung in der Natur und ist der göttliche Teilung (lat. proportio divina) genannt.
Die Ganze ist mehr als die Summe seiner Teile. Die Schale des Nautilus beinhaltet in ihrem Aufbau sowohl
die Fibonacci-Zahlen und
den goldenen Schnitt, als auch das Prinzip der Selbstähnlichkeit: Ihr Wachstum lässt sich durch Quadrate ausdrücken, deren Seitenlänge sich aus der Summe der beiden nächstkleineren Quadrate ergibt. Zählen wir nach. 2+3=5; 3+5=8; 5+8=13... usw. Der Nautilus ist mehr als die Summe seiner Teile, der Nautilus ist ein Lebewesen das sich, dank seiner Körperbau, bewegen und verteidigen kann. Die Natur hat von Anfang an, mit dem Gesetz des goldenen Schnittes und aus ihm entwickelten Körperbau, die Entstehung der Arten geordnet und verteidigt. Die Ganze entstehet aus der Bewegungsdynamik seiner Teile.
Pentagramm
Das Pentagramm, eines der ältesten magischen Symbole der Kulturgeschichte, steht in einer besonders engen Beziehung zum Goldenen Schnitt.
Die 5 (die Länge des kürzeren Abschnitts) verhält sich zur 8 (die Länge des längeren Abschnitts) in etwa so, wie die 8 sich zur 13 (die Länge der Summen dieser beiden Abschnitte) verhält.
Die Fibronacci-Zahlenreiche ist auch da 5, 8, 13, 21.
Zu jeder Strecke und Teilstrecke im Pentagramm findet sich ein Partner, der mit ihr im Verhältnis des Goldenen Schnitts steht.
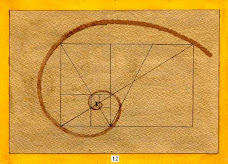
Rechteck
Länge und Breite eines Rechtecks teilen sich im Verhältnis des Goldenen Schnittes. Überträgt man nun die Breite auf die Längsseite, so entstehen ein Quadrat und ein kleineres Rechteck, in dem sich wiederum Länge und Breite stetig teilen. Die Zusammensetzung von Viertelkreisen in den Quadraten erzeugt die Goldene Spirale. Das Ende der Spirale, ihrer letzten Punkt sollten wir uns als Mitte des Gelenks, als der Anfang oder der Drehepunkt der Bewegung Vorstehellen können. Wenn ich aus der richtigen Ausgangsstellung meines Körpers meinen Arm ausstrecke um nach etwas zu greifen, dann habe ich mit meiner Armbewegung die Wege drei goldenen Spiralen erreicht und so die dynamische Bewegungsgeometrie gestaltet.
Ich kann aus jedem Derieck mit hilfe des Rechtecks wieder ein Pentagram zeichnen.
Die Entstehung des goldenen Schnittes in meinem Körper
Das Pentagramm lässt sich auch als aus fünf Goldenen Dreiecken zusammengesetzt denken. Verbindet man die fünf Schnittpunkte im Inneren, so entsteht dort ein weiteres Pentagramm. Selbst wenn man in dessen innerem Fünfeck wieder ein Pentagramm einzeichnet und so fort, sind sämtliche in dieser Zeichnung auffindbaren Dreiecke Goldene Dreiecke.
Der Goldene Schnitt ist ein Harmoniegesetz, dessen grundlegende Bedeutung sich seit Jahrtausenden nicht geändert hat. Die Kenntnis dieses Gesetzes gibt all den Menschen ein überaus sinnvolles Hilfsmittel in die Hand, die in irgendeiner Form gestalterisch tätig sind.
Die übersichtliche und verständliche Darstellung umfasst die geschichtlichen und künstlerischen Gegebenheiten des Themas ebenso wie Fragen nach der Anwendung des Gesetzes. Ich habe in meinen Überlegungen der Gestz des goldene Schnittes zuerst in meinem Körper gesucht. Das mit einer irrationale Zahl ausgedruktes mathematischer Gesetz musste ich denken lernen. Dabei half mir die Proprtionslehre des Polyklet und Vitruvius.
Proportionen des menschlichen Körpers
Die wohl bedeutendste Proportionlehre der Griechen stammt von Polyklet 5. Jh. v.Chr. Er hat eine allerdings nicht erhaltene Proportionschrift "Kanon"(Regel) geschrieben und eine plastische Figur nach dieser Regel geschaffen, die auch nicht im Original erhalten ist, den Doryphoros oder Speerträger. Polyklet war offenbar der Erste, der seine Theorie auf Messungen am menschlichen Körper zurückgeführt hat.
Wiederhollen wir. Der Goldene Schnitt ist ein Harmoniegesetz zur Erzielung von Harmonischen Proportionen. Es beruht auf der Teilung einer Linie in 2 ungleiche Teile, wobei sich der kleinere Teil (c, Minor) zum grösseren Teil (b, Major) gleich verhält, wie der größere zur Summe beider Teile (a).
Doryphorus oder der Speerträger und der goldener Schnitt.
Wir treffen im menschlichen Körper auf den Goldenen Schnitt. Dieser findet sich zum Beispiel im Verhältnis von
Das dieser Streckenteilung mehr zugrunde liegt als reine Willkür, liegt nahe. Es handelt sich dabei um ein seit mehreren Jahrtausenden bekanntes und angewandtes Proportionverhältnis.
Seit eher haben sich Wissenschaftler, Künstler und Andere dafür interessiert, nach welchen Regeln und Grundlagen sich Proportionen in der Natur verhalten.
Der Goldene Schnitt beschreibt somit jenes Teilungverhältnis, welches in vielen Bereichen in der Natur dem Wachstum, der Bewegung und dem natürlichen Kräftespiel zugrunde liegt. Das dieses Verhältnis für unsere menschliche Wahrnehmung harmonisch erscheint, ist daher nicht weiter verwunderlich.
Nach Platon ist der Mensch das Wesen, das "Gefühl für Ordnungen und Unordnung in den Bewegungen hat, für das also, was man als Rhythmus und Harmonie bezeichnet". Es geht also nicht um abstrakte Massverhältnisse, sondern um den organischen Aufbau des Ganzen, zunächst des menschlichen Körpers, dann aber auch um den lebendigen Zusammenhang des menschlichen Mikrowelt und schliesslich mit dem Universum überhaupt.
Der Mensch als das "Mass der Dinge" (Protagoras, 480 - 410 v Chr.) war Vorbild für die Proportionen des griechischen Tempels:
"Wenn man sich also darüber einig ist, dass die Zahlenordnung von den Gliedern des Menschen hergeleitet ist, und dass zwischen den einzelnen Gliedern und der Gesamterscheinung des Körpers eine entsprechende, auf einem Grundmass (modulus) beruhende Symmetrie besteht, bleibt nur übrig, dass wir denjenigen Anerkennung zollen, die beim Bau der Tempel ... die Glieder ihrer Werke so geordnet haben, dass mit Hilfe von Proportionen und Symmetrie (richtigem und schönen Massverhältnis) deren Gliederungen im Einzelnen wie im Ganzen zueinander passend geschaffen wurden." (Vitruv, de architectura, entstanden ab 33 v. Chr., III. Buch).
Vitruvs System wurde von Proportiontheoretikern der Renaissance übernommen, so z.B. von Leonardo da Vinci. Sein "Homo ad Circulum" ist eine Illustration der Vitruvschen Proportionlehre. Er übernimmt die Aussage Vitruvs, dass der Nabel der "Mittelpunkt" des Körpers sei, aber Leonardo bestätigte mit seiner Zeichnung noch etwas: "Die Grösse des Körpers ist gleich der Länge den beiden ausgestrecktem Armen." Leonardo da Vinci hat in seinen Skizen mit den Bewegungen des Mannes die Qudratur des Kreises dargestellt.
http://www.klaus-schroeer.com/publish/schroeer-irle-leonardo-da-vinci/content/02-03/02-03.html
Der Goldene schnitt und die Bewegung.
Die Ansicht der Goldene Schnitt sei ein göttliches Naturgesetz der in vielfacher Weise in den Proportionen des menschlichen Körpers realisiert ist gibt mir die Möglichkeit dieser gestz in der menschlichen Bewegungen zu suchen. Ohne das wir dass bewusst wahrnehmen jede Bewegung unseres Körpers beschreibt im Raum eine Spirale. Der Mensch ist ein Teil der Natur und die Natur kennt keinen geraden Linien der Bewegung. Die vierte Dimension, der Zeit erleubt das nicht. Ich versuchte die Zeit die ich brauche für die Ausführung einer Bewegung meines Armes wahrzunehmen. Die Dauer der Bewegung und der Gewicht meines Körperteils krümmte den Raum und ich stellte fest mein Arm hat das Gesetz des goldenen Schnittes befolgt und auf seinem Weg zur Kaffetasse der Spuhr der goldenen Spirale hinterlassen.
In jedem Mensch steckt ein Tänzer, schreibt Rudolf von Laban in seinem Buch "Choreutik" und ich habe versucht seine Bewegungsprache zu verstehen.
"Die menschliche Kinesphäre die durch die Bewegungen in eine Dynamosphäre verwandelt wird. Nicht der Raum des Kubus’ um uns herum begrenzt und sichert damit die eigene Bewegungssphäre, sondern es reizen und fordern gerade die Punkte uns, die knapp und weiter ausserhalb dieser Kinesphäre liegen, die Grenze zu überschreiten und die Möglichkeiten des Bewegens des Körpers in Raum und Zeit zu erproben. Das kann mit den Gliedmassen geschehen, mit den Gelenken von Schulter oder Hüfte, mit dem Kopf, der Nase oder dem Ohr … und das findet innerhalb der drei Ebenen des eigenen Körpers statt: der oben, der unten und der der eigenen Mitte, und auf und in allen Ebenen des Raums. Es provoziert ein Bewegen, das unerkannte und unbewusste Punkte und Sphären des Raums um uns herum eröffnet, unsere Wahrnehmung erweitert und dabei, also im Bewegen, unsere Aufmerksamkeit darauf lenkt und sie schärft, was mit anderen Teilen unseres Körpers passiert, etwa des Rumpfes, des Kopfes oder des Halses sowie der Wirbelsäule im Ganzen." Choreograph und Tanzpädagoge Rudolph von Laban.
Die Kinesphäre des Menschen und die darin enthaltenen Bewegungsrichtungen, die immer mit einer Spiralbewegung des Körpers ausgeführt werden. Das sind die für uns und für die Anderen nicht sichtbare Spuren unseren Bewegungen im Raum, aber wir sehen die Bewegung des Körpers und geben ihr eine Name. Wir gehen, absitzen und aufstehen, kleiden uns an und aus, putzen, bügeln, essen und trinken, wir spielen Tennis, schwimmen oder Tanzen. Das sind alles die Bewegungen die durch die Geometrie unseres Körperbaus die Arhitektur unseres Daseins gestalten.
Das Ikosaäder ist der komplexeste geometrische Körper. Es besteht aus 20 Dreiecken - und an jeder Ecke stossen 5 Kanten und 5 Flächen zusammen. Es ist also von der Zahl 5 bestimmt; und die Fünf mit dem zugehörigen Goldenen Schnitt eröffnet von den Geheimlehren der Pythagoräer bis zur neuesten mathematischen Forschung ein weites Feld für Zahlenmystik.
Die Bewegungen im Ikosaeder bedeuten eine dynamische Kristallographie der menschlichen Bewegung, also ein Symbol für die Übereinstimmung von organischer Natur und abstraktem mathematisch-geometrischem Gesetz und für die Vereinigung von feststehenden und dynamischen, starren und veränderlichen Elementen.
Ikosaeder befinden sich die drei goldenen Rechtecke versteckt.
Wenn man die Winkel im Ikosaäder, die der menschliche Körper in seinen normalen Alltagsbewegungen beschreibt, vergleicht, kommen wir zu den Schlussfolgerung das zwischen die Winkel des Ikosaäder und den Winkeln in denen sich die Körperglieder bewegen die Übereinstimmung herscht. Es ist auch bemerkenswert, dass das Verhältnis zwischen der Länge der dimensionalen und diagonalen Transversalen des Ikosaäder und die Länge seiner Oberflächenlinien dem Gesetz des goldenen Schnitts folgt.
Stellen Sie sich ihren persönlichen Raum als ein Ikosaeder vor und versuchen Sie jede Ecke des imaginären geometrischen Körpers als Ausgangspunkt ihrer Bewegung zu visualisieren. Die Baustruktur des Ikosaeders gleicht der Baustruktur des Kristalls. Jetzt versuchen Sie den starren Körper des Ikosaeders sich als ein Kristall vorzustellen.
Der Kristall ist die lebendige Architektur der Natur die in ihrer Baustruktur die Spirale aus Unzeligen Tetraeder verbirgt. Ihre Bewegungen im Ikosaeder werden dann gleich der dynamischen Kristallographie der menschlichen Bewegung. Der Kristall ist ein Symbol für die Übereinstimmung von organischer Natur und abstraktem mathematisch-geometrischem Gesetz und für die Vereinigung von feststehenden und dynamischen, starren und veränderlichen Elementen. Ihre Bewegungen sind Spiralförmig und Sie befolgen mit jeder Ihren Bewegung die Naturgesetze des Kristallbau welcher in seiner Entstehung den Gesetz des goldenen Schnittes befolgt.
Das Gesetz des goldenen Schnitts ist ein wichtiger Gesetz in der Arhitektur des Raumes und findet auch im menschlichen Körperbau statt.
Der Nabel teilt die Körpergrösse im Verhältnis des Goldenen Schnitts, und der untere Abschnitt ist durch das Knie auch so geteilt. Ferner scheinen die Verhältnisse benachbarter Teile der Gliedmassen wie beispielsweise bei Ober- und Unterarm sowie bei den Fingerknochen ungefähr in diesem Verhältnis zu stehen. Eine genaue Überprüfung ergibt jedoch Streuungen des Verhältnisses im 20-Prozent-Bereich. Oft enthält auch die Definition, wie beispielsweise die Länge eines Körperteils exakt zu bestimmen sei, eine gewisse Portion Willkür. Ferner fehlt dieser These bis heute eine wissenschaftliche Grundlage.
Das Teilungsverhältnis eines Rechtecks der in den Fibonacci-Zahlen 1, 1, 2, 3, 5, 8, 13, 21, 34 usw., dargestellt ist, und jede nachfolgende Zahl nach 1 gleich der Summe der beiden vorhergehenden Zahlen ist. Bei dividieren zwei benachbarte Zahlen entstähet das Verhältnis - 1:1.618 - des Goldenen Schnittes. Wenn Sie jedes kleinere Rechteck noch einmal mit dem gleichen Verhältnis dividieren und die Ecken verbinden, erhalten Sie eine logarhitmische Spirale, genannt die goldene Spirale. So entstehet die goldene Spirale, die uns den Weg der Wachstumsbewegung unseres Körper zeigt und uns gleichzeitig zur bewusste Wahrnehmung der dynamischen Raum- Zeitdimension in der Natur und damit auch in uns selbst führt.
Der Architekt Le Corbusier (1887-1965) entwickelte zwischen 1942 und 1955 ein universelles Masssystem, den sogenannten Modulor. Der Modulor stellte den Versuch dar, der Architektur eine am Mass des Menschen orientierte mathematische Ordnung zu geben. Ausgehend vom Goldenen Schnitt und von den Proportionen des menschlichen Körpers entwickelte Le Corbusier seine Proportionslehre des Bauens. Er ging von einer angenommenen Standardgrösse des menschlichen Körpers aus und markierte drei Intervalle, die zueinander in der Proportion des Goldenen Schnitts stehen. Dabei versuchte er wie damals Leonardo da Vinci den Kreis zu Qudrieren.
Seine Proportionfigur wurde bekannt unter dem Namen "
Modulor" und diente dem Architekten zur Findung von Massen am Bau.
Die Bewegungen des Mensches folgen in ihren Entstehungen das Gesetz des goldenen Schnittes seines Körperbau und hinterlassen in den Raum die Spure der goldenen Spirale. Um das zu verstehen müssen wir uns jeden bewegenden Teil des Körpers als ein Rechteck in dem Raum einer Kugel vorstellen können.
Ich stelle mir mein Arm als drei Rechtecken vor: der Oberarm, Unterarm und die Hand. Um die Bewegungsgeometrie meines Arms bei den Alltagsbewegungen zu sichern stelle ich mir in Gedanken die Bilder der goldenen Spirale vor. Das kleinste Rechteck befindet sich immer in dem Zentrum des Schulter, Ellenbogen oder Handgelenkes. Die Bewegung meines Arms breitet sich aus dem Schluttergelenk wie eine goldenen Spirale aus. In dem Ellenbogen ändert sie die Richtung und bretitet sich weiter zum Handgelenk als dopell Spirale aus. Im Handgelenk ändert sie wieder die Richtung und so ist aus der goldene Spirale die dynamische Spirale meiner Armbewegung geworden.
Die Seuerung der Bewegung findet in meinem Kopf statt, dort wo sich auch den goldenen Schnitt folgend die goldene Spirale in eine dynamische Spirale verwandelt.
Schweizer Briefmarke zu Ehren des Goldenen Schnittes;
Stephan Bundi. Der Gesetz des goldenen Schnittes finden wir auch in unserem Kopf. Ende der goldenen Spirale in unserem Kopf ist der Punkt wo man in dem cartesianischem Theater den Beobachter sucht und die gottes Augen nennt.
Die Natur kennt keine ruhigen Augenblicke, keine unbeweglichen Materie und keinen verlust der Energie.
Die Bewegung ist der höhste Priester der Natur. Unsere Körper und Bewegungsgeometrie sind aus den Naturgesetzen entstanden und in unsere Raum- Zeitdimension verschmolzen. Wir sollten die Entstehung unserer Gesundheit in uns selber und in der Natur und Philosophie die unser Dasein bestimmen, suchen.
Die Haltung ist kein statischer Dasein unseres Körpers, die ist ein dynamischer Prozess und von einem zum anderen Augenblick, veränderbar. Wenn wir stehen bleiben um uns von langem Laufen zu erholen in unserem Körper wirbeln tausende kleine goldnene Spiralen, die uns unsere aufrechte Stand ermögllichen.
Der goldene Schnitt und die Schönheit
Der goldene Schnitt lehrt uns, dass das Irrationale und das Nichtrechenbare Bestandteil der Natur sind, die Symmetrie und Nichtsymmetrie die Schönheit gestallten, nicht jedoch im Sinne des Unharmonischen und Hässlichen, sondern als Teil des Schönen und Wunderbaren. Dank dem Gesetzt des goldenen Schnittes, wir können die Prinzipien der Natur erfassen und sogar das Schöne als "eine Manifestation für uns noch immer geheimer Naturgesetze" verstehen. Als Teil des Ganzen können wir aber nicht die Natur der Ganzheit und somit auch nich die Schönheit entzaubern, denn "... sie schafft ewig neue Gestalten; was da ist, war noch nie; was war, kommt nicht wieder – alles ist neu und doch immer das Alte." (Goethes Werke 1893).
Jene für den Menschen maximal erscheinenden Widersprüche verbildlicht der goldene Schnitt in einem weiteren Gegensatz, nämlich im mathematischen Modell von »Symmetrie« und »Asymmetrie«. Während die Symmetrie offenkundig eine grosse Nähe zum sogenannten Schönen hat, erweist sich auch die Asymmetrie des goldenen Schnitts als eine Darstellungsseite des Schönen.
http://www.golden-section.eu/„Asymmetrie macht das Phänomen“ Pierre Curie
Hinzu kommt schliesslich der Gegensatz von »Subjektivismus« und »Objektivismus«, welche in
der Proportio divina eine Gemeinsamkeit finden. Das subjektive Schönheitsempfinden des Menschen, welches in der Kunst und in der Architektonik klassischer Bauten zum Ausdruck kommt, bringt genauso die Proportionen des goldenen Schnittes zum Vorschein, wie das objektive Entwicklungsmuster der Natur in Form der Fibonacci-Reihe.
Die Symbiose der Gegensätze, wie sie der goldene Schnitt verwirklicht, erzeugt den Ausdruck vollendeter Harmonie und Schönheit. Der Grund ist eine allem zugrundeliegende Ganzheit. Diese erhebt sich über den maximalen Widerspruch der verschiedenartigen Gegensätze zur Komplementarität. Der Bezug jedes einzelnen Teiles (Minor und Major) zum Ganzen schafft im Betrachter ein Bild der Einheit und Vollkommenheit. Schönheit ist demnach im Sinne des goldenen Schnittes das Erkennen des unauflöslichen Zusammenhangs vom Ganzen und seiner Teile. Schönheit ist ein Ausdruck des Ganzen durch die Integration zweier scheinbar unvereinbarer Gegensätze.
»Das Gleichnis dessen, der die höchste Vernunft besitzt, ist und kann nur die Fähigkeit sein, die Beziehungen zu erkennen, die auch Dinge einen, die scheinbar keinerlei Verbindungen zueinander haben.« (Pythagoras)
Der oberste Ziel des Kinesitherapeuten ist beim Patient der Bewegungablauf der Anfang, die Dauer und das Ende der Bewegung, also die vierdimensionale Eigenmobilisation, bewusst zu machen und durch den Bewegungsbewusstsein die Heilung, die Beseitigung oder Linderung der Schmerzsymptome des Bewegungssystems und die Wiederherstellung seiner Harmonie um damit seinen Funktionen zu verbessern.
Ich stelle mir mein Arm als drei Rechtecken vor: der Oberarm, der Unterarm und die Hand. Um die Bewegungsgeometrie meines Arms bei den Alltagsbewegungen zu sichern stelle ich mir in Gedanken die Bilder der goldenen Spirale vor. Das kleinste Rechteck befindet sich immer in dem Zentrum des Schulter, Ellenbogen oder Handgelenkes.
Sie wird oft, wie in obenstehender Abbildung, durch eine Folge von Viertelkreisen approximiert. Die Zusammensetzung von Viertelkreisen in den Quadraten erzeugt die logarithmische Spirale. Sie ist eine Spirale, die mit jeder Umdrehung den Abstand von ihrem Mittelpunkt, dem Pol, um den gleichen Faktor vergrössert. In umgekehrter Drehrichtung schlingt sich die Kurve mit abnehmendem Radius immer enger um den Pol. Jede Gerade durch den Pol schneidet die logarithmische Spirale stets unter dem gleichen Winkel.
Ich stelle mir mein Arm als drei Rechtecken vor: der Oberarm, der Unterarm und die Hand. Um die Bewegungsgeometrie meines Arms bei den Alltagsbewegungen zu sichern stelle ich mir in Gedanken die Bilder der goldenen Spirale vor. Das kleinste Rechteck befindet sich immer in dem Zentrum des Schulter, Ellenbogen oder Handgelenkes.
